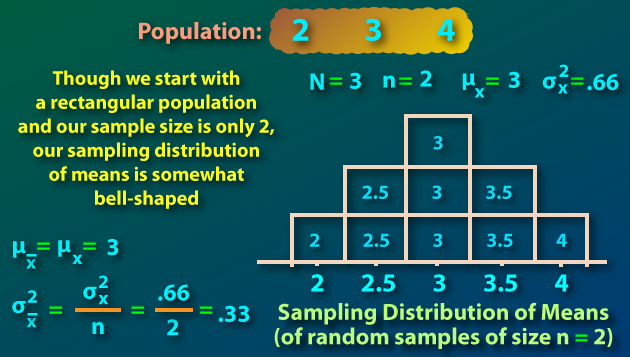
The Central Limit Theorem is a statement about the characteristics of the sampling distribution of means of random samples from a given population. That is, it describes the characteristics of the distribution of values we would obtain if we were able to draw an infinite number of random samples of a given size from a given population and we calculated the mean of each sample.
[1] The mean of the sampling distribution of means is equal to the mean of the population from which the samples were drawn.
[2] The variance of the sampling distribution of means is equal to the variance of the population from which the samples were drawn divided by the size of the samples.
[3] If the original population is distributed normally (i.e. it is bell shaped), the sampling distribution of means will also be normal. If the original population is not normally distributed, the sampling distribution of means will increasingly approximate a normal distribution as sample size increases (i.e. when increasingly large samples are drawn).
The accompanying figure illustrates the statements of the Central Limit Theorem both algebraically and graphically.